Cuerpo negro y catástrofe ultravioleta. 5

cuerpo negro
 en Física  Etiquetado Física y tecnología cuántica / Un poco de por

Durante los últimos años del siglo XIX la Física se encontraba en medio de un periodo efervescente. Las leyes de Maxwell aún no se habían asimilado completamente, al igual que las implicaciones de las Leyes de la termodinámica. Las patas de la Física estaban empezando a crecer y multiplicarse y la comunidad científica comenzaba a dividirse. En este marco los filamentos de las bombillas empezaron a iluminar el mundo y algunas mentes brillantes se plantearon como era posible que esos pequeños alambres difundieran una luz tan constante en intensidad y color.

Ya se sabía que el color de emisión de los cuerpos incandescentes dependía de la temperatura a la que se encontraba dicho cuerpo. El hierro de las fraguas cambiaba de color al calentarse y enfriarse. Por lo que la radiación que emite un objeto tiene una frecuencia de emisión dependiente de la temperatura, siendo más rojizos los cuerpos calientes y más azules los fríos. La fórmula por lo tanto era fuertemente dependiente de la temperatura. R(T).

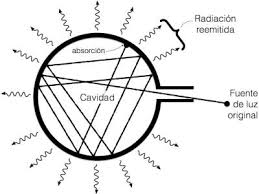
cuerpo negro
Modelo de un cuerpo negro

Para poder profundizar en las matemáticas de la ecuación se necesita más que los colores de un acero incandescente. Fue Gustav Kirchhoff (1824-1887) el que planteo el sistema de medición perfecto. El cuerpo negro. Pero era tan perfecto que era irrealizable.

El cuerpo negro es un objeto negro con una pequeña apertura por la que entra la radiación exterior. Una vez dentro esta sufre varias reflexiones hasta que se absorbe por completo. Al mismo tiempo, las radiaciones que se emiten cubren todas las longitudes de onda por lo que se puede considerar como un emisor perfecto. Siempre dependiendo de la temperatura.

Con esta construcción mental, Kirchhoff solo pudo demostrar la dependencia de la temperatura. Sin datos experimentales no podía avanzar más. Al fin y al cabo el cuerpo negro era solo una entelequia.

En 1879, Josef Stefan (1835-1893) analizando los datos demostró que la densidad de la radiación era dependiente de la cuarta potencia de la temperatura. Y la dependencia era constante. La formulación parecía encajar bien y Ludwig Edward Boltzmann (1844-1906), utilizando las ecuaciones de Maxwell y de la termodinámica, consiguió demostrarlo teóricamente. La formulación matemática quedaba como E = σT4, siendo σ la constante de Stefan-Boltzmann. 

Poco tiempo después, el físico Wilhelm Wien (1864-1928) formuló matemáticamente la relación entre la radiación emitida y la longitud de onda para una determinada temperatura. Haciendo uso de conceptos estadísticos, Wien concluyó que al calentar el cuerpo negro el punto máximo de la curva en la distribución espectral se desplaza hacia longitudes de onda más cortas. Hacia el rojo. Esta nueva formulación relacionaba las longitudes de onda con la temperatura de forma constante. Así, conocido el pico de radiación a una temperatura, podíamos conocer la longitud de onda máxima del resto de temperaturas. Este resultado pasó a ser la ley de desplazamiento de la curva de la densidad de energía de la cavidad de un cuerpo negro. (λmax=0,0028976m·K/T)

Pocos años después, Wien completaría su trabajo teórico con la formulación de una ley para el problema del cuerpo negro. Friedrich Paschen (1865-1947) se encargaría de comprobar experimentalmente esta nueva ley de distribución para longitudes de onda cortas y Otto Lummer (1960-1925) ampliaría el espectro con un nuevo cuerpo negro experimental.

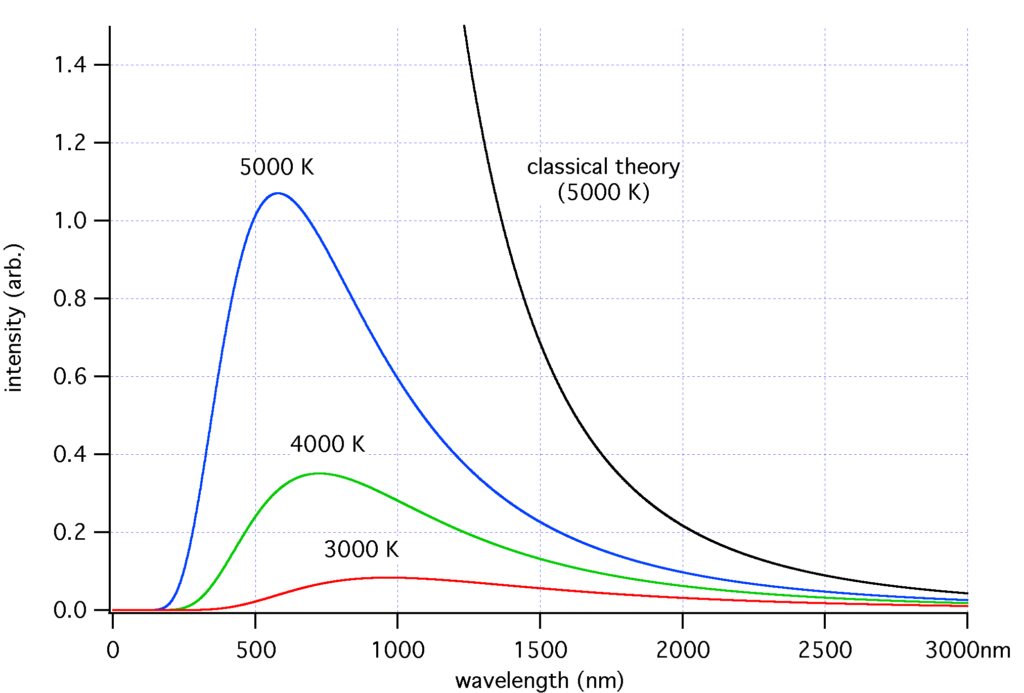
Además de Wien, Max Planck (1858-1947) estaba muy interesado en la demostración experimental de la esta expresión matemática que parecía resistirse en la región de los infrarrojos. Planck intentaba unir las matemáticas de Wien con las leyes de la termodinámica como contraposición al teorema de equipartición de Lord Rayleigh (1842-1919) y James Jeans (1877-1946). Este teorema dividía la radiación del cuerpo negro en secciones según la longitud de onda, pero solo parecía ajustarse correctamente en las longitudes de baja frecuencia. Las condiciones para que se cumpliera este teorema era que el gas estuviera distribuido uniformemente por el espacio y que solo pudiera moverse en tres direcciones con seis grados de libertad (3 de traslación y 3 de rotación). El modelo era bueno, pero en la región del ultravioleta los datos teóricos diferían desastrosamente con los experimentales. A esta discrepancia se la denomino “Catástrofe ultravioleta”.

Si la fórmula de Rayleigh-Jeans fuera correcta, la energía radiada por el cuerpo negro crecería exponencialmente hasta el infinito con la longitud de onda y sabemos que no es cierto. Por eso Planck estaba tan interesado en el camino abierto por Wien. No podía aceptarse una fórmula que originaba una catástrofe ultravioleta.

Planck recurrió a los osciladores armónicos como emisores de radiación para su cuerpo negro teórico e intentó repartir la energía entre ellos. Pero no fue capaz hasta que recurrió a una idea que presento Boltzmann y que él había rechazado. La de que los osciladores absorbían y emitían paquetes de energía a los que llamó cuantos y describió como h·ν. A Planck no le gustaba nada la idea de la existencia de estos cuantos, pero era la forma de obtener una ecuación matemática que se ajustase a los datos experimentales en todo el espectro.

En este punto entra Einstein en el problema del cuerpo negro. Se da cuenta de que Planck no había aplicado toda la teoría de Boltzmann sobre los paquetes de energía, y que si lo hubiera hecho, hubiera llegado a una nueva catástrofe ultravioleta.

El problema de la radiación del cuerpo negro parecía no tener solución dentro de la Física conocida.

cuerpo negro
Radiación de un cuerpo negro

Como Einstein había trabajado con las relaciones electromagnéticas no fue tan reacio a asumir la discretización de la energía. Unificó todos los trabajos y teorías, las junto con la termodinámica y el electromagnetismo, y los aplicó sobre átomos en vez de partículas de gas. El cuerpo negro de Einstein formado por partículas se ajustaba a la distribución de paquetes o cuantos de luz.

Después de varios años y científicos, la definición de los cuantos de luz fue la solución al problema del cuerpo negro. Esta solución cerraba un debate, pero era el germen de toda una nueva física que había que descubrir. Una nueva rama insinuada por Planck que nunca llegó a aceptarla y recogida por un Einstein al que superó. Esta nueva física, no demostrable experimentalmente pero que se ajustaba a los problemas conocidos. Sobre la que se debía creer ciegamente haciendo ejercicios de imaginación muy radicales en aquellos años. Una nueva rama que encontró adeptos y críticos. Era el principio de una nueva era.



Referencias: