FT: Función de Transferencia 6

A la hora de trabajar con sistemas de control, la mejor herramienta del analista es la Función de Transferencia o FT. Esta función matemática contiene toda la información del sistema que se quiere controlar, de su planta, de los errores y de los sensores. Es una modelización mediante ecuaciones de todo lo que ocurre dentro del sistema como respuesta a la entrada de una señal.

Está definida como la respuesta de un sistema ante una entrada dada. Esta definición se debe a que su representación es la transformada de Laplace de la función que modela la salida dividida por la de la entrada. Suponiendo que las condiciones iniciales son nulas.

G(s)=Y(s)/X(s)

Este tipo de modelado matemático se aplica a los sistemas lineales invariantes en el tiempo.

Conociendo un sistema, podemos modelizarlo para obtener las ecuaciones que lo describen, y, aplicando la transformada de Laplace, obtener la FT. De la misma forma, conociendo la FT, podemos deducir el sistema de control.

La transformada de Laplace, F(s), es un operador matemático que calcula la integral semi-infinita de una función, y que se emplea sobre todo para la resolución de ecuaciones integrales. Sus propiedades matemáticas la convierten en un operador robusto y versátil para la resolución de sistemas de ecuaciones.

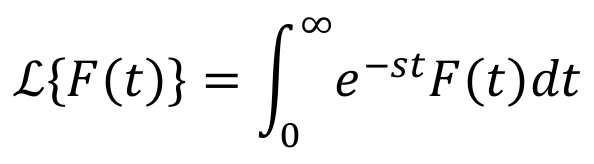
El orden de la función de transferencia está definido por el denominador. Por lo tanto el grado del polinomio característico de la salida es el orden tanto de la FT como de la ecuación diferencial asociada. Se dice que un sistema es de orden mínimo si no se cancelan los polos y los ceros en la FT. Mientras que se califica de propio si el orden del numerador es menor o igual que el del denominador, y de estrictamente propio si es menor. La mayoría de los sistemas reales tiene una FT propia.

Estabilidad de los sistemas

Dada una FT, podemos hacer un estudio de la estabilidad del sistema mediante el análisis de los polos y los ceros de una función compleja. Este análisis, dependiendo del tipo de sistema de control que se esté utilizando, puede ser extrapolable a sistemas reales o solo será aplicable a modelos ideales. Pero sea extrapolable o no, es una buena aproximación para saber si el control diseñado se puede o no ajustar a las especificaciones de estabilidad.

Para analizar la estabilidad por el método de polos y ceros, siendo los polos las raíces de la función denominador, [X(s)=0], y los ceros de la del numerador, [Y(s)=0], primero factorizamos las transformadas de Laplace. Después “pintamos” sobre un sistema de ejes real e imaginario dichas raíces. Si encontramos un polo en el semiplano derecho la FT del sistema es inestable. Mientras que si encontramos ceros en dicho semiplano, aunque el sistema presente zonas de inestabilidad, será finalmente estable.

Existen otros métodos de análisis de estabilidad de sistemas que se pueden aplicar a las funciones de transferencia como el el Criterio de estabilidad de Nyquist y el Criterio de estabilidad de Routh-Hurwitz.

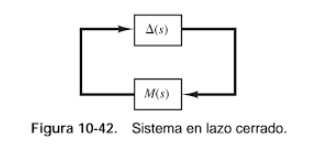
Diagramas de bloques y modelado por FT

Mediante el análisis de los pares de datos entrada/salida de un sistema se puede conocer la FT característica del control. Los diagramas de Bode, por ejemplo, son un buen método para obtener dichas Funciones de Transferencia en el dominio de la frecuencia. En este dominio se realiza una transformación tal que s=ωj.

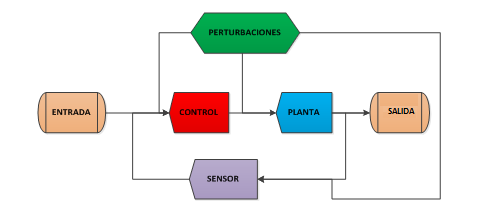
El uso de las funciones de transferencia para describir no solo la planta del sistema de control, sino también los diferentes componentes como los sensores, es la clave para entender la modelización por diagrama de bloques tan característica de los Sistemas de control modernos.

La caracterización de los sistemas de control eléctricos está perfectamente definida con el uso te las transformadas de Laplace y de las FT. Cada tipo de componente eléctrico tiene asociado una función determinada, por lo que los cálculos y los análisis son muy simples de realizar.

La FT es por tanto una herramienta muy potente y completa en la Ingeniería de Control cuando los sistemas son invariantes en el tiempo. Simplifica tanto el modelado como los análisis y cálculos necesarios además de caracterizar perfectamente los sistemas físicos. Es reversible ya que podemos obtener la FT del sistema o el sistema de la FT. Y es estocástico, por lo que se puede tabular para simplificar los cálculos y diseños.

Referencias:

• Ingeniería de control moderna. K. Ogata. Pearson. 5º Edición.
• https://www.monografias.com/trabajos106/funcion-transferencia-sistemas-lineales/funcion-transferencia-sistemas-lineales.shtml
• https://euler.us.es/~renato/clases/mm2/laplace.pdf