Cuando un robot se desplaza autónomamente tiene que ser capaz de evitar los obstáculos de su camino. Si mandamos un robot al interior de una habitación para realizar una misión, debemos estar seguros de que no se chocará con una silla y no pueda realizarla. Existen varias estrategias para lograr que el robot se desplace sin problemas. Pero pueden agruparse en dos tipos. Uno es in situ, mediante sensores que detecten los obstáculos y un software con retroalimentación. Otra es con un análisis previo. Mediante el estudio de mapas se puede obtener el camino más óptimo. Realizando una planificación de caminos.
La planificación de caminos es muy importante en robótica. Grafos, gráficos de visibilidad, descomposiciones espaciales, etc. En este artículo vamos a analizar el que se basa en los Diagramas de Voronoi.
Los Diagramas o Teselaciones de Voronoi se llaman así debido al matemático ruso llamado Georgy Voronoi (1868-1908). También son llamados Polígonos de Thiessen o Teselación de Dirichlet, debido a científicos que también realizaron estudios sobre esta materia.
Dado un espacio en el que se encuentra situados varios puntos de interés, Voronoi divide dicho espacio en secciones que se sitúan bajo la influencia de cada punto. Matemáticamente se define como la unión de los puntos del plano más cercanos a un punto dado.
Si nos centramos en las dos dimensiones del plano, las regiones de Voronoi son aquellas que se encuentran más cercanas de cada punto en el plano. Para calcularla estas regiones, vale con trazar las mediatrices entre los puntos de interés (perpendiculares a los segmentos que unen los puntos trazados en el medio de estos). Si tenemos dos puntos el plano quedaría dividido por el punto medio.

Si son tres:
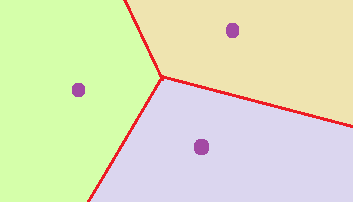
Y para un espacio de muchos puntos:

Como peculiaridad se puede decir que los puntos cuyas regiones son colindantes cortan a la misma circunferencia con centro en el vértice de intersección.
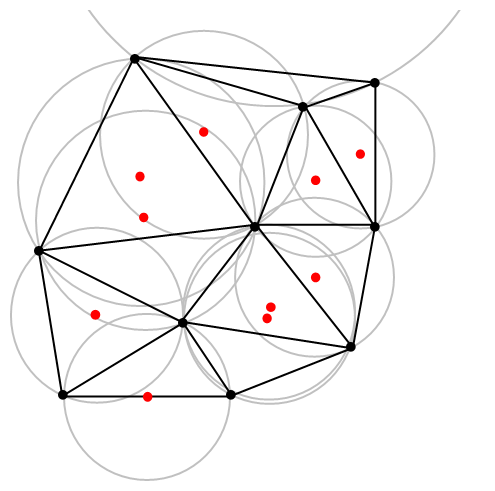
Si tenemos en cuenta que la condición de Delaunay de un triángulo es que la circunferencia circunscrita del mismo no debe contener ningún otro vértice de la triangulación en su interior, podemos triangular la región del espacio. Por lo tanto los Diagramas de Voronoi y la triangulación de Delaunay son duales en el espacio.

En un espacio de tres dimensiones, 3D, el resultado obtenido es parecido al de llenar un espacio con pompas de jabón.
Volviendo a la robótica, se aplica Voronoi a los mapas para obtener rutas óptimas de desplazamiento. Si las regiones descritas por los Diagramas son el conjunto de puntos más cercano a los puntos, las líneas que los delimitan son los más lejanos de cada punto. Al aplicar Voronoi a la planificación de caminos, la ruta que garantiza un camino sin obstáculos es aquel que se forma al unir las mediatrices.
Por lo tanto, dado el mapa de espacio a recorrer, primero se aplica un ensanchamiento de seguridad a los contornos de los objetos para simplificar el trazado y evitar aristas. Después se unen los vértices y otros puntos de interés y se trazan las mediatrices de los segmentos. El camino que asegura que el robot se encuentre lo más alejado de los obstáculos en todo momento será el que marquen dichas mediatrices.
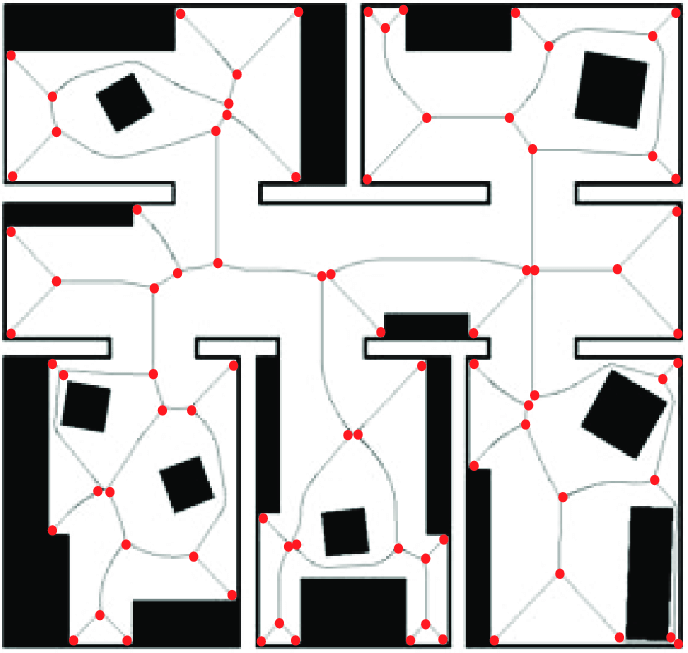
Este método es simple e intuitivo. Los algoritmos que deben calcular el camino óptimo para el desplazamiento del robot no son complejos y por lo tanto no necesitaran de grandes recursos hardware. Solo necesitas el plano del recorrido. Y este puede obtenerse y digitalizarse de muchas maneras.
Los Diagramas de Voronoi tienen muchas aplicaciones. Gracias a su simplicidad pueden ser aplicados a un gran número de problemas de representación espacial. Desde realizar distribuciones de terrenos conocer zonas de influencia para por ejemplo controlar plagas o diseñar sistemas de navegación con algoritmos de planificación de caminos. Estos diagramas son una herramienta experimental muy útil.
Referencias:
- Apuntes de la asignatura de Robótica de la carrera de Ingeniería Electronica de la UCM.
- https://naukas.com/2011/12/23/cada-uno-en-su-region-y-voronoi-en-la-de-todos/

